



Originally published in the Slide Rule Gazette, Issue 17, Autumn 2016 with subsequent addition
In days of yore before electric motors became cheap and commonplace in factories for driving machinery, it was frequently driven by steam. Compared to electric motors steam engines were large, cumbersome beasts with associated boilers that had to be fed with coal (or in later years with oil or gas). It was not practical to have one by each machine and instead the steam engine would be centrally located and the power transmitted to the machines by a system of ropes, pulleys and belts. One of the principal makers of driving ropes in the UK was Thomas Hart of the Lambeth Rope Works, Blackburn, England.

Figure 1 - The Thomas Hart advert in the 14 th (1916) Edition of Pickworth
Thomas Hart was a regular advertiser in Pickworth and other engineering manuals. In my first article on Lambeth cotton driving rope calculators I illustrated and described a calculator with this name that was used to find the rope driving horsepower, rope speed, and diameters and speeds of pulleys. This free, card slide rule given away by Thomas Hart was essentially a design tool for the rope drive itself.
It came as somewhat a surprise to find another slide rule for sale on eBay (subsequently won by David Rance) with the same title but for a very different purpose. It is similar in construction to the first and has a similar paper envelope to protect it. However this one is used to calculate the power of the steam engine itself. It is illustrated in figures 2 and 3.
It came as somewhat a surprise to find another slide rule for sale on eBay (subsequently won by David Rance) with the same title but for a very different purpose. It is similar in construction to the first and has a similar paper envelope to protect it. However this one is used to calculate the power of the steam engine itself. It is illustrated in figures 2 and 3.


Figure 3 – the reverse side of the calculator © D Rance
Its main purpose is to calculate the indicated horsepower of the steam engine knowing its piston speed, cylinder diameter, and the mean effective pressure. Now the relation between these in Imperial units is
IHP = Pm.L.A.N/33000 where Pm is the mean effective pressure in pounds per square inch, L is the piston stroke in feet, A is the cylinder area in square inches (that needs to be multiplied by 2 if the engine is double acting), and N is the speed in revolutions per minute.
The mean effective pressure is normally measured using an engine indicator. This has been described in an earlier article of mine on the Thornton 6039½ slide rule.
IHP = Pm.L.A.N/33000 where Pm is the mean effective pressure in pounds per square inch, L is the piston stroke in feet, A is the cylinder area in square inches (that needs to be multiplied by 2 if the engine is double acting), and N is the speed in revolutions per minute.
The mean effective pressure is normally measured using an engine indicator. This has been described in an earlier article of mine on the Thornton 6039½ slide rule.
Looking at the slide rule, the scales are annotated D / C , B / A where:
D = Indicated Horse Power (reciprocal 2000–20
C = Piston Speed – Feet per Minute (reciprocal 4000–40)
B = Mean Effective Pressure – Lbs per Sq. In. (2-200)
A = Cylinder Diameter – Inches (reciprocal 100-10)
D = Indicated Horse Power (reciprocal 2000–20
C = Piston Speed – Feet per Minute (reciprocal 4000–40)
B = Mean Effective Pressure – Lbs per Sq. In. (2-
A = Cylinder Diameter – Inches (reciprocal 100-
It is quite a basic slide rule and slightly awkward to use as the piston speed, which is clearly not constant, has to be calculated first from the stroke and rpm. However this can be calculated using this slide rule as described in the instructions at the bottom of the front face.
These state: “TO FIND INDICATED HORSEPOWER:- Set Mean Effective Pressure on B line to Cylinder Diameter on A line and over Piston Speed on C line, read IHP on D. TO FIND PISTON SPEED:- Set Stroke in Inches on B to Arrow PS and over Revolutions per Minute on C, read Piston Speed on D, then proceed as before.”
These state: “TO FIND INDICATED HORSEPOWER:-
It is annotated “Copyright” and “Entr’d at Stationers Hall” and there is an acknowledgement to C N Pickworth, DFI, Manchester. Now Pickworth produced a steam engine horsepower calculator himself that I previously described in my paper on Hudson’s Computing Scales.
Figure 2 – The upper side of the calculator © D Rance
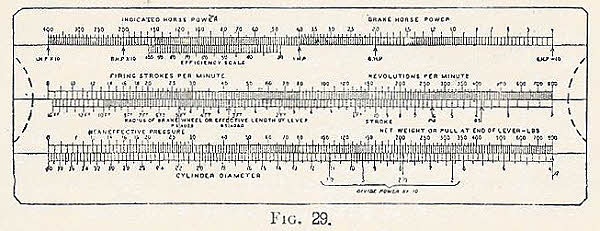
Figure 4 – Pickworth’s Engine Power Computer (Pickworth, 14th Edition)
This is a rather more complex slide rule having two slides. This was available for many years; for example it is listed in A G Thornton’s 1916 catalogue in cardboard, priced at 5/- It also includes Brake Horsepower on the horsepower scale, Net Weight of Pull on the Mean Pressure Scale, and an Efficiency scale. It could be used for low speed oil and gas engines (using firing strokes per minute instead of revolutions) as well as steam engines, and could calculate brake horsepower from dynamometer data.
However, let us return to the Lambeth Cotton Driving Rope calculator. On the reverse, below its advertisement for Hart’s ropes, there is a useful table. For rope diameters from 1 to 2 inches in 1/8 inch steps it gives weight per yard in pounds and ounces, and maximum horsepower per rope. They are stated to be the highest advisable powers for ropes running at the most advantageous speeds of 3,600 to 5,000 feet per minute and in the most advantageous situations. Interestingly the maximum horsepower of a 1 3/8 inch diameter rope is 28 – exactly the same figure as that given by the Cooper Cotton Driving Rope Gauge described in the previous article (reference ii). In fact the tables (and figures) are the same throughout except that the Cooper one does not give the weights.
Returning to the upper side, does the slide rule give the right answer? To find out I printed the picture and pasted it to card to make a simple replica. For my test I assumed a steam engine with the following properties:
However, let us return to the Lambeth Cotton Driving Rope calculator. On the reverse, below its advertisement for Hart’s ropes, there is a useful table. For rope diameters from 1 to 2 inches in 1/8 inch steps it gives weight per yard in pounds and ounces, and maximum horsepower per rope. They are stated to be the highest advisable powers for ropes running at the most advantageous speeds of 3,600 to 5,000 feet per minute and in the most advantageous situations. Interestingly the maximum horsepower of a 1 3/8 inch diameter rope is 28 – exactly the same figure as that given by the Cooper Cotton Driving Rope Gauge described in the previous article (reference ii). In fact the tables (and figures) are the same throughout except that the Cooper one does not give the weights.
Returning to the upper side, does the slide rule give the right answer? To find out I printed the picture and pasted it to card to make a simple replica. For my test I assumed a steam engine with the following properties:
Stroke = 20 inches
RPM = 60
Mean effective pressure = 40 psi
Cylinder diameter = 16 inches
This results in: Piston speed = 200 ft/min, and thence IHP = 51
Using the formula Pm.L.A.N/33000 gave an answer of 24.3 which when doubled gives IHP = 48.6 so it seems very likely that the calculator assumes the engine will be double acting. This would be a very reasonable assumption as this would be the usual case for a mill engine at the time this calculator was produced.
Why is Pickworth acknowledged on the Lambeth calculator? It is much more basic than the Pickworth slide rule and that itself appears to be an elaboration of the Hudson Horsepower Computing Scale that predated the Pickworth, it would appear, by at least 15 years. Both the Hudson & the Pickworth have two slides whilst the Lambeth has only one. Did Pickworth design this more basic slide rule specially for Thomas Hart?
Postscript: Just after this article had appeared in print a third Lambeth Cotton Driving Rope Horse Power Calculator appeared on eBay and I acquired it. The upper, slide rule, face is identical to that shown in Figure 2. but the reverse face is entirely different with further tables comparing English and metric weights and measures rather than rope illustrations, It is shown in Figure 5 below.
Why is Pickworth acknowledged on the Lambeth calculator? It is much more basic than the Pickworth slide rule and that itself appears to be an elaboration of the Hudson Horsepower Computing Scale that predated the Pickworth, it would appear, by at least 15 years. Both the Hudson & the Pickworth have two slides whilst the Lambeth has only one. Did Pickworth design this more basic slide rule specially for Thomas Hart?
Postscript: Just after this article had appeared in print a third Lambeth Cotton Driving Rope Horse Power Calculator appeared on eBay and I acquired it. The upper, slide rule, face is identical to that shown in Figure 2. but the reverse face is entirely different with further tables comparing English and metric weights and measures rather than rope illustrations, It is shown in Figure 5 below.
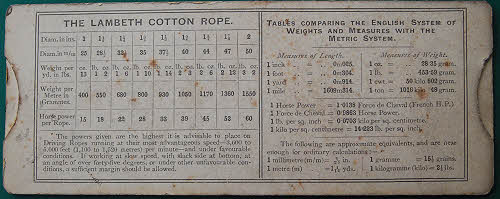
Figure 5 – the reverse side of the third calculator
Acknowledgements
My thanks are due to David Rance for providing the information on this second type of Lambeth Cotton Driving Rope Horsepower Calculator and the excellent pictures of it.
| Early Sets |
| Traditional Sets |
| Later Sets |
| Major Makers |
| Instruments |
| Miscellanea |
| W F Stanley |
| A G Thornton |
| W H Harling |
| Elliott Bros |
| J Halden |
| Riefler |
| E O Richter |
| Kern, Aarau |
| Keuffel & Esser |
| Compasses |
| Pocket compasses |
| Beam compasses |
| Dividers |
| Proportional dividers |
| Pens |
| Pencils |
| Rules |
| Protractors |
| Squares |
| Parallels |
| Pantographs |
| Sectors |
| Planimeters |
| Map Measurers |
| Miscellaneous |
| Materials Used |
| Who made them |
| Who made these |
| Addiator |
| Addimult |
| Other German |
| USA |
| Miscellaneous |
| Microscopes |
| Barometers |
| Hydrometers & Scales |
| Pedometers |
| Surveying Instruments |
| Other instruments |
| Workshop Measuring Tools |
| Catalogues & Brochures |
| Micrometers & Verniers |
| Engineering rules and gauges |
| Wood rules & calipers |
| Dial gauges & miscellaneous |